
Зимни математически състезания - Бургас, 2007
Време за работа – 4 часа.
4 Клас
Задача 1. Двадесет на брой петици са записани една след друга: 5 5 5 ... 5 5. Напишете между някои от цифрите знака „+”, така че полученият сбор да е равен на 1000. (За цифрите, между които не е написан знак, считаме, че образуват едно число.)
Задача 2. Числата 2, 7, 12, 17, 22, 27, ..., 2002, 2007 са записани по следното правило: след всяко число записваме сбора му с 5, докато стигнем до 2007. Колко числа са записани?
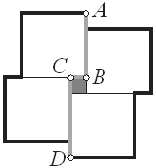
Задача 3. Фигурата на чертежа е съставена от четири големи квадрата с равни страни и един малък квадрат. Страната на всеки от големите квадрати е 4 пъти по-голяма от страната на малкия квадрат и дължината на начупената линия АВCD е 30 см. Да се намерят лицето и обиколката на получената фигура.
Задача 4. Запишете върху всяко картонче по една цифра, така че едновременно да са изпълнени шестте равенства.
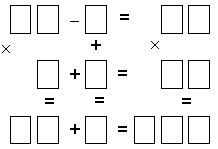
5 Клас
Задача 1. Да се реши ребусът А.ДДА = ДУУМ:А , където на различните букви съответстват различни цифри.
Задача 2. В цирка имали три костюма за клоуни от риза, панталони и обувки. Единият костюм бил син, втория – червен, а третия – зелен. Клоуните АН, БАН и ВАН разбъркали костюмите и се появили на арената облечени така: ризата и обувките на АН били в един и същи цвят; ВАН не носел нищо червено; обувките на БАН били зелени, а ризата и панталоните в другите два цвята. Какъв e цветът на ризата, панталоните и обувките на всеки от тях?
Задача 3. Плочка Г-тетрамино  се състои от 4 еднакви квадратчета със страна 3 см. Такива плочки са наредени една до друга, както е показано:
се състои от 4 еднакви квадратчета със страна 3 см. Такива плочки са наредени една до друга, както е показано:

а) Ако броят на плочките е 2007, да се намерят лицето и обиколката на получената фигура. б) Ако обиколката на фигурата е 7002 см, да се намери лицето й.
Задача 4. Етапът “Светофар” в рали за минимобили е дълъг 9 км. На втория километър има светофар, който свети 3 мин. зелено, 3 мин. червено, 3 мин. зелено и т.н. На четвъртия километър светофарът свети 2 мин. зелено, 1 мин. червено, 2 мин. зелено и т.н. Третият светофар е разположен на шестия километър и свети 4,5 мин. зелено, 5,5 мин. червено, 4,5 мин. зелено и т. н. Всеки минимобил стартира точно в момента, когато и трите светофара светнат едновременно червено, като няма право да спира или да променя скоростта си до финала.
Минимобилът “Еко” стартирал в 10 ч. 45 мин. и изминал етапа, без да нарушава правилата, за възможно най-малкото време. В колко часa е финиширал “Еко” и с каква скорост (километри в час) се е движил?
6 клас
Задача 1. В един паркинг броят на червените коли е 25% от всички коли. В продължение на един час от паркинга излизат и влизат коли , като в края на часа се оказало, че броят на паркираните коли се е увеличил с 3, а червените коли представляват 12% от всички паркирани коли. Какъв най-малък брой коли са били паркирани първоначално и колко от тях са били червени?
Задача 2. Да се намерят всички двойки естествени числа m и n, за които е изпълнено 1! + 2! + 3! + L + n! = m2.
(с n! се означава произведението на естествените числа от 1 до n: n! = 1.2.3.L.(n-1).n)
Задача 3. В триъгълника АВС точка Р е средата на страната ВС, а точка Т е от страната АС и AT = 4TC. Отсечките АР и ВТ се пресичат в точка М. Да се намери каква част от лицето на четириъгълника ТМРС е лицето на триъгълника СРМ.
Задача 4. На дъската е записано числото 4608. Всяка минута числото от дъската се умножава или дели (само ако делението е възможно без остатък) на 2 или на 3. Резултатът се записва на дъската, а старото число се изтрива. Възможно ли е точно след 33 часа и 27 минути на дъската да е записано числото 27? След най-малко колко минути числото 27 може да се появи на дъската?
7 клас
Задача 1. В 9 часа от пристанище А към пристанище В срещу течението на река, което има скорост 3 км/ч, тръгнала моторна лодка. Два часа и двадесет минути след тръгването двигателят на лодката спрял поради повреда и на екипажа били необходими 1 час и 20 минути, за да приведе отново лодката в движение. След повредата двигателят загубил част от мощността си и собствената скорост на лодката се намалила с 25%. Лодката пристигнала в В 2 часа и 48 минути след възобновяване на движението. Да се намери собствената скорост на лодката в спокойна вода преди повредата и разстоянието между А и В, ако разстоянието изминато преди повредата е със 7 км повече от разстоянието, изминато след отстраняването на повредата.
Задача 2. Даден е квадрат ABCD със страна a. Точките M и N лежат съответно върху страните BC и CD и са такива, че S MAN = 45° . Да се намери периметърът на триъгълника MNC.
Задача 3. Да се намери най-малкото естествено число k, за което уравнението
x12 + x22 + ... + xk2 = 2007
има решение в множеството на естествените числа.
Задача 4. Множеството Е се състои от 37 двуцифрени числа, нито едно от които не се дели на 10. Да се докаже, че в Е могат да се намерят 5 числа такива, че за всеки две от тях цифрите на десетиците са различни и цифрите на единиците са различни.
8 клас
Задача 1. Дадено е уравнението |2x - 1| - 1 = x2 - a. а) Да се реши уравнението при a = 2. б) Да се намерят стойностите на параметъра а, за които уравнението има два корена, които са цели числа.
Задача 2. Числата x и y са такива, че x(4 - 3x) + y(4 - 3y) = 3xy.
Да се докаже, че
0 ≤ x + y ≤ 16/9
Задача 3. В триъгълника ABC S ACB = 2S ABC. Точката M лежи върху страната AC, такава че CM = BC. Да се намерят ъглите на триъгълника ABC, ако BM = AC.
Задача 4. В квадратна таблица 2007 x 2007 са записани цели неотрицателни числа така, че ако числото в една клетка е 0, то сборът от числата в реда и стълба, които се пресичат в тази клетка е не по-малък от 2007. Да се докаже, че сборът от всички числа в таблицата е не по-малък от 2 014 025.